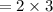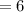Question

What is the length of the conjugate axis?

Answer 1

It's 6 haha

Explanation:

The length of the conjugate axis is found by finding the value of "b" then multiplying it by 2 because the value of the conjugate axis is 2b. Ik I'm super late hahaha but I hope this helped, thanks for the points!

Answer 2

ANSWER

The length of the conjugate axis is 6 units.

EXPLANATION

The given hyperbola has equation:


`((x - 1)^(2) )/(25) - \frac{ {(y + 3)}^(2) }{9} = 1`

We can rewrite this equation in the form:


`\frac{(x - 1)^(2) }{ {5}^(2) } - \frac{ {(y + 3)}^(2) }{ {3}^(2) } = 1`

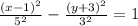
We compare this equation to:


`\frac{(x - h)^(2) }{ {a}^(2) } - \frac{ {(y - k)}^(2) }{ {b}^(2) } = 1`

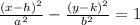
This implies that;


`a = 5`

and


`b = 3`

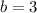
The length of the conjugate axis of a hyperbola is


`= 2b`

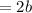
Substitute b=3 to obtain;


`= 2 * 3`


`= 6`