Hello!
The answer is:
d)
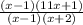
Why?
A hole is a point where rational functions lose its continuity, meaning that in that point, there is a discontinuity condition.
We can find the hole of a rational function if there are similar terms on the numerator and the denominator by finding:
First (x-component): The values of x that makes the function equal to 0 in both numerator and denominator.
Second (y-component): Re-evaluating the same term in the other factors of the function to know the y-component.
Finding the x component we have:
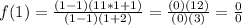
So, the x-component is 1,
Then, re-evaluating the function:
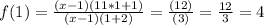
Therefore, the y-component is 4,
Hence,
The function has a hole at (1,4)
Have a nice day!