Answer:
The height of cylinder is 10 meters.
Explanation:
Given
Curved Surface Area = 44m^2
Radius = r = 0.7 m
The curved surface area of a cylinder is given by:
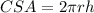
Putting the values we get
Pi can be taken as 22/7 or 3.14
We are taking 22/7 for the question
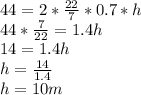
Hence,
The height of cylinder is 10 meters.