Hello!
The answer is:
c.
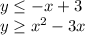
Why?
Let's check if the given inequalities match with the given graph
First, finding the axis intercepts:
For the first inequality:
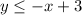
x-axis intercept:
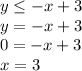
y-axis intercept:
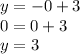
So, the function intercepts the x-axis at 3 and the y-axis at 3
Interception points, for (0,3) and (3,0)
According to the inequality, the solution for the inequality is below the line.
For the second inequality:
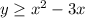
x-axis intercept:
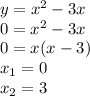
y-axis intercept:
Since there is not "c", the parabola intercepts the y-axis at 0
Interception points, (0,0) and (3,0)
According to the inequality, the solution for the inequality is above the parabola.
Hence,
The solution for the system of inequalities will be the area between both inequalities solutions, below the line and above the parabola, it means that the correct option for the graph is:
c.
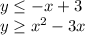
Have a nice day!