Answer: OPTION A.
Explanation:
Some tranformations for a function f(x):
If
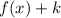 , then the function is shifted up "k" units.
, then the function is shifted up "k" units.
If
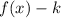 , then the function is shifted down "k" units.
, then the function is shifted down "k" units.
If
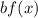 , and
, and
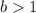 , then the function is vertically stretched by a factor of "b".
, then the function is vertically stretched by a factor of "b".
If
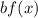 , and
, and
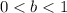 , then the function is vertically compressed by a factor of "b".
, then the function is vertically compressed by a factor of "b".
If
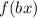 , and
, and
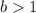 , then the function is horizontally compressed by a factor of
, then the function is horizontally compressed by a factor of
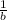
If
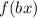 , and
, and
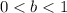 , then the function is horizontally stretched by a factor of
, then the function is horizontally stretched by a factor of
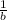
Since the function f(x) is:
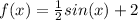
And the function g(x) is:

You can observe that the function g(x) is the function f(x) but shifted up 6 units and vertically stretched by a factor of 4.