For this case we have that by definition, the area of a circle is given by:
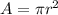
Where,
We have then that the radio is given by:
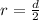
Where,
- d: diameter of the circle
Substituting values we have:
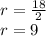
Then, calculating the area we have:
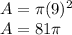
Answer:
on a circular serving tray that has a diameter of 18 in can be placed:
