Question

Ella invested $2,700 in an account paying an interest rate of 5.4% compounded

monthly. Assuming no deposits or withdrawals are made, how long would it take, to
the nearest year, for the value of the account to reach $4,020?

Answer 1

7

Explanation:

Answer 2

The account will take 7 years to reach a value of $4,020

Explanation:

Compound Interest

When it occurs interest in the next period is then earned on the principal sum plus previously accumulated interest.

The formula is:

`{\displaystyle A=P\left(1+{\frac {r}{n}}\right)^(nt)}`

Where:

A = final amount

P = initial principal balance

r = interest rate

n = number of times interest applied per time period

t = number of time periods elapsed

Ella invested P=$2,700 in an account with an interest rate of r=5.4% (0.054) compounded monthly. Since there are 12 months in a year, n=12.

It will be calculated when will the account have a value of A=$4,020. Substituting all the values in the formula:

`{\displaystyle 4,020=2,700\left(1+{\frac {0.054}{12}}\right)^(12t)}`

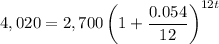
Calculating:

`{\displaystyle 4,020=2,700\left(1.0045)^(12t)}`

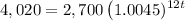
Dividing by 2,700:

`{\displaystyle (4,020)/(2,700)=\left(1.0045)^(12t)}`

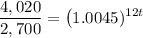
To solve this equation for t, we need to apply logarithms:

`{\displaystyle \log(4,020)/(2,700)=\log\left(1.0045)^(12t)}`

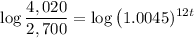
Applying the logarithm power rule:

`\displaystyle \log(4,020)/(2,700)=12t\log 1.0045`

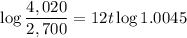
Dividing by 12log 1.0045:

`\displaystyle t=(\log(4,020)/(2,700))/(12\log 1.0045)`

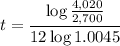
Calculating:

t= 7.39 years

Rounding to the nearest year, the account will take 7 years to reach a value of $4,020