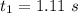Question

Theo's flying disc got stuck in a tree 14 feet from the ground. Theo threw his shoe up at the disc to dislodge it. The height in feet h of the shoe is given by the equation h= -16^2+25t+6, where t is the time in seconds. Determine whether the shoe hit the disc. Use the discriminant to explain your answer.

Answer 1

The shoe hit the disc.

Explanation:

Let
`ax ^ 2 + bx + c` be a quadratic function where a, b and c are the real coefficients of the function.

Then the discriminant of the function is:

`b ^ 2 - 4ac`

The result of this expression gives us information about the roots of this equation.

* If the discriminant is > 0 then the equation has 2 real solutions

* If the discriminant is > 0 then the equation has 2 complex solutions

* If the discriminant is = 0 then the equation has 1 real solution.

For this case we have the equation:

`h = -16t ^ 2 + 25t + 6`

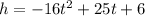
If we assume that the shoe reached the disc, then
`h = 14\ ft`

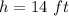
So:

`14 = -16t ^ 2 + 25t + 6`

`-16t ^ 2 + 25t + 6 -14 = 0\\\\-16t ^ 2 + 25t -8 = 0\\\\a = -16\\\\b = 25\\\\c = -8`

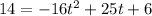
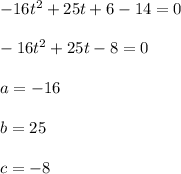
Then the discriminant is:

`25^2 -4(-16)(- 8) = 113`

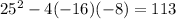
The discriminant is greater than 0. Then the equation has 2 real solutions.
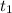`t_1` and
`t_2`.

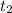This means that if there are values ​​of t for which
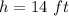`h = 14\ ft`. In other words, this means that the shoe reached the disc.

In fact if you use the quadratic formula to solve the equation you will get:

`t_1 = 1.11\ s`

`t_2 = 0.450\ s`