Answer:

Explanation:
To solve this problem we must calculate the discriminant of each quadratic function.
Let
 be a quadratic function with a, b and c their real coefficients, then:
be a quadratic function with a, b and c their real coefficients, then:
If
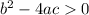 the function has 2 real solutions.
the function has 2 real solutions.
If
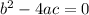 the function has 1 double real solution
the function has 1 double real solution
If
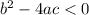 the function has complex solutions.
the function has complex solutions.
Now we calculate the discriminant for each of the functions:
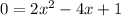
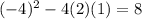 (Two real solutions)
(Two real solutions)
-----------------------------------------------------------------------------------
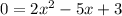
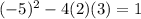 (Two real solutions)
(Two real solutions)
------------------------------------------------------------------------------------

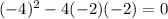 (A real double solution)
(A real double solution)
------------------------------------------------------------------------------------

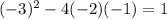 (Two real solutions)
(Two real solutions)
-----------------------------------------------------------------------------------
The equation we want is:
