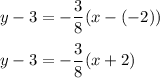Answer:
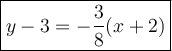
Explanation:
Ths point-slope form of an equation of a line:
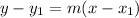
m - slope
(x₁, y₁) - point
We have the equation:
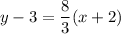
Therefore the slope is
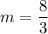
Let k: y = m₁x + b₁ and l: y = m₂x + b₂.
l ⊥ k ⇔ m₁m₂ = -1 ⇒ m₂ = -1/m₁
Therefore
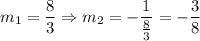
The line passes throguh the point (-2, 3).
We have the equation in point-slope form: