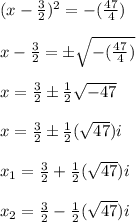Question

Solve each quadratic equation by completing the square. Give exact answers--no decimals.

Answer 1

x= 3/2 +(√47) i / 2 , x = 3/2-(√47) i / 2

Explanation:

We have given the equation :

x² -3x +14 = 0

We have to find the value of x.

x² -3x +14 = 0

x²-3x = -14

x² -2(x)(3/2) +(3/2)² = -14 +(3/2)²

(x - 3/2)² = -14 + 9/4

(x - 3/2)² = -47/4

Squaring both sides we get,

(x-3/2) = ±√ -47/4

(x-3/2) = ±(√47) i / 2

x = 3/2 ± (√47) i / 2

x= 3/2 +(√47) i / 2 or x = 3/2-(√47) i / 2 is the answer.

Answer 2

`x_1 = (3)/(2) + (1)/(2)(√(47))i\\\\x_2 = (3)/(2) - (1)/(2)(√(47))i\\\\`

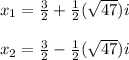
Explanation:

In this problem we have the equation of the following quadratic equation and we want to solve it using the method of square completion:

`x ^ 2 -3x +14 = 0`

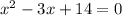
The steps are shown below:

For any equation of the form:
`ax ^ 2 + bx + c = 0`

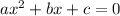
1. If the coefficient a is different from 1, then take a as a common factor.

In this case
`a = 1`.

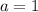Then we go directly to step 2

2. Take the coefficient b that accompanies the variable x. In this case the coefficient is -3. Then, divide by 2 and the result squared it.

We have:

`(-3)/(2) = -(3)/(2)\\\\(-(3)/(2)) ^ 2 = ((9)/(4))`

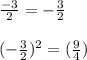
3. Add the term obtained in the previous step on both sides of equality:

`x ^ 2 -3x + ((9)/(4)) = -14 + ((9)/(4))`

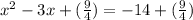
4. Factor the resulting expression, and you will get:

`(x -(3)/(2)) ^ 2 = -((47)/(4))`

Now solve the equation:

Note that the term
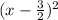`(x -(3)/(2)) ^ 2` is always > 0 therefore it can not be equal to
`-((47)/(4))`

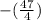
The equation has no solution in real numbers.

In the same way we can find the complex roots:

`(x -(3)/(2)) ^ 2 = -((47)/(4))\\\\x -(3)/(2) = \±\sqrt{-((47)/(4))}\\\\x  = (3)/(2) \±(1)/(2)√(-47)\\\\x = (3)/(2) \±(1)/(2)(√(47))i\\\\x_1 = (3)/(2) + (1)/(2)(√(47))i\\\\x_2 = (3)/(2) - (1)/(2)(√(47))i\\\\`