Question

How to solve this problem​

Answer 1

Let C be the center of the circle. The measure of arc VSU is
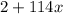`2+114x`, so the measure of the minor arc VU is
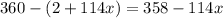`360-(2+114x)=358-114x`. The central angle VCU also has measure
`358-114x`.

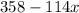Triangle CUV is isosceles, so the angles CVU and CUV are congruent. The interior angles of any triangle are supplementary (they add to 180 degrees) so

`m\angle VCU+2m\angle CUV=180`

`\implies m\angle CUV=\frac{180-(358-114x)}2=57x-89`

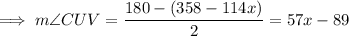
UT is tangent to the circle, so CU is perpendicular to UT. Angles CUV and VUT are complementary, so

`(57x-89)+(31x+3)=90`

`\implies88x=176`

`\implies x=2`

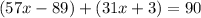
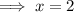
So finally,

`m\widehat{VSU}=2+114\cdot2=230`

degrees.