Question

The exponential function f(x) = 2x undergoes two transformations to

g(x) = 1/3• 2x – 7. How does the graph change? Select all that apply.
A. It is shifted right.
B. It is shifted down.
C. It is flipped over the x-axis.
D. It is vertically compressed.
E. It is vertically stretched.

Answer 1

shifting down

vertically compressed

Explanation:

Answer 2

Shifting down.

Vertically compressed

Explanation:

Given

`f(x) = 2^x`

`g(x) = (1)/(3)(2^x - 7)`

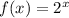
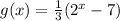
Required

Determine the translation from f(x) to g(x)

The first translation from f(x) towards g(x) is:

`f(x) = 2^x`

`f'(x) = 2^x - 7`

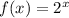
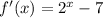
This is derived by:

`f'(x) = f(x) - b`

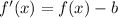
Where

`b = 7`

Notice that, in the above, b (i.e. 7) was subtracted from f(x), this implies that the function shifted down

The next translation that resulted in g(x) is:

`g(x) = (1)/(3)(2^x - 7)`

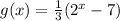
This is derived by:

`g(x) = a.f'(x)`

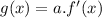
By comparison:

`a = (1)/(3)`

Since the value of a is less than 1, then f'(x) is vertically compressed to give g(x).

Hence, the transformations that apply from f(x) to g(x) are:

• Shifting down.

• Vertically compressed