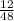Answer:
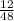
Explanation:
You know that the ratio of the numerator to the denominator of the fraction is 1:4. This can be written as
 . Then you can write the following expression
. Then you can write the following expression
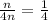
Where the denumerator is 4 times the numerator.
You also know that if you add three to the numerator and subtracted from the denominator, the new fraction reduces to
 :
:

Then, you must solve for n, as following:
\
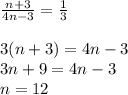
Then the denominator is:
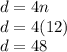
The original fraction is: