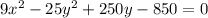Question

identify the graph of 9x^2-25y^2=225 for t(0 5) and write an equation of the translated or rotated graph in general form

Answer 1

It's C) hyperbola; 9x^2-25y^2+250y-850=0

Answer 2

The required equation is:

`9 {x}^(2) - 25{y}^(2) + 250y - 85 0=0`

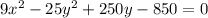
Step-by-step explanation

The given equation is

`9 {x}^(2) - 25 {y}^(2) = 225`

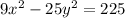
Dividing through by 225 we obtain;

`\frac{ {x}^(2) }{25} - \frac{ {y}^(2) }{9} = 1`

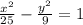
This is a hyperbola that has it's centre at the origin.

If this hyperbola is translated so that its center is now at (0,5).

Then its equation becomes:

`\frac{ {(x - 0)}^(2) }{25} - \frac{ {(y - 5)}^(2) }{9} = 1`

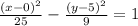
We multiply through by 225 to get;

`9 {x}^(2) - 25( {y - 5})^(2) = 225`

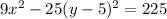
We now expand to get;

`9 {x}^(2) - 25( {y}^(2) - 10y + 25 )= 225`

`9 {x}^(2) - 25{y}^(2) + 250y - 6 25 = 225`

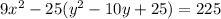
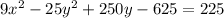
The equation of the hyperbola in general form is

`9 {x}^(2) - 25{y}^(2) + 250y - 85 0=0`