Question

How many solutions exist for the system below?

In two or more complete sentences, give the solution and explain how you solved the system.
{ y=-2x+3
{y=-2(3^x)

Answer 1

​The system of equations has no solution. Geometrically speaking, both the lines will never intersect or meet. Hence, no solution exists.

Explanation:

Answer 2

There are no solutions to this system. If

`-2x+3 > 0 \iff x < (3)/(2)`

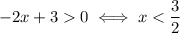
the line is positive and the exponential is negative, so they can't have any point in common.

At
`x = (3)/(2)`, the derivative of the line is
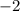`-2`, whereas the derivative of the exponential is
`-3^x\log(9)`.

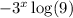Since
`-3^x\log(9)<-2` for all
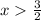`x>(3)/(2)`, there can't be other solutions because the exponential is already below the line, and it decreases at a faster rate.