Question

Assume that there are 2 trials.

X = 2 where X represents the number of successes.



Which probability matches the probability histogram?

Round the answer to one decimal place.



P(success)=0.2

P(success)=0.3

P(success)=0.7

P(success)=0.8

Answer 1

P(success) = 0.2

This is the correct answer to this problem! I just took the test! Good luck!!

Answer 2

P(success)=0.2 matches the probability histogram.

Explanation:

Formula :
`P(X)=^nC_r p^r(1-p)^(n-r)`

Where X represents the number of successes.

p represents probability of success .

1-p represents probability of failure.

Now when X= 0 the probability is 0.64 (Using histogram )

So,
`^2C_0 p^0(1-p)^(2)=0.64`

`(1-p)^(2)=0.64`

`(1-p)=√(0.64)`

`(1-p)=0.8`

`1-0.8=p`

`0.2=p`

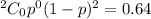
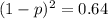
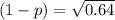
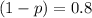
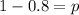
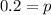
So, the probability of success = 0.2

Hence P(success)=0.2 matches the probability histogram.