Question

I don’t know how to do this

Answer 1

To check for continuity at the edges of each piece, you need to consider the limit as
`x` approaches the edges. For example,

`g(x)=\begin{cases}2x+5&\text{for }x\le-3\\x^2-10&\text{for }x>-3\end{cases}`

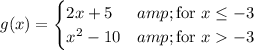
has two pieces,
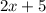`2x+5` and
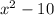`x^2-10`, both of which are continuous by themselves on the provided intervals. In order for
`g` to be continuous everywhere, we need to have

`\displaystyle\lim_(x\to-3^-)g(x)=\lim_(x\to-3^+)g(x)=g(-3)`

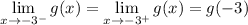
By definition of
`g`, we have
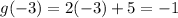`g(-3)=2(-3)+5=-1`, and the limits are

`\displaystyle\lim_(x\to-3^-)g(x)=\lim_(x\to-3)(2x+5)=-1`

`\displaystyle\lim_(x\to-3^+)g(x)=\lim_(x\to-3)(x^2-10)=-1`

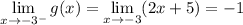
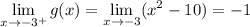
The limits match, so
`g` is continuous.

For the others: Each of the individual pieces of
`f,h` are continuous functions on their domains, so you just need to check the value of each piece at the edge of each subinterval.