Question

In a parallelogram ABCD, AC ~ BD . Is ABCD a rectangle ?

Answer 1

yes it is a rectangle

Answer 2

Yes

Explanation:

ABCD is a parallelogram

By definition of parallelogram

AB=CD, BC=AD

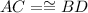`AC=\cong BD`...(given)

AB=AB

Reflexive property

AD=BC (By definition of parallelogram)

`\triangle`ABC
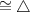`\cong\triangle`ABD

Reason: SAS postulate

`\angle A=\angle B`

Reason:CPCT

We know that in parllelogram

Sum of same side interior angle=180 degrees

`\angle A+\angle B=180`

`\angle A+\angle A=180`

`2\angle A=180`

`\angle A=(180)/(2)=90^(\circ)`

`B=\angle 90^(\circ)`

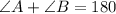
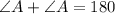
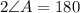
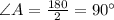
We know that

Opposite angles of parallelogram are equal

`\angle A=\angle C, \angle B=\angle D`

`\angle A=\angle B=\angle C=\angle D=90^(\circ)`

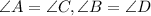
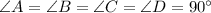
In rectangle , Opposite sides of rectangle are equal and each angle is of 90 degrees.

Therefore, by definition of rectangle

ABCD is a rectangle.

Hence, proved.