Answer:
+5
Explanation:
Let's analyze the sine function first:

we know that this is periodic function with values between -1 and 1.
Now let's consider the function of the problem
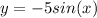
Here we have basically multiplied the previous function by a constant number, -5. Therefore, we have:
- when

- when
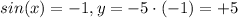
So, the values of the function
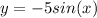
are between -5 and +5, and so its maximum value is +5.