Question

Graph each absolute value function. State the domain, range, and y-intercept.

Answer 1

i) D: All real numbers

ii) R:
`y\ge2`

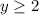
iii) Y-int: b=2.25

Explanation:

i) The given absolute value function is

`y=(1)/(4)|x+1|+2`

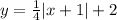
The domain is all values of x that makes the function defined.

The absolute value function is defined for all values of x.

The domain is all real numbers.

ii) The given function is
`y=(1)/(4)|x+1|+2`

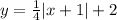
The function has vertex
`(-1,2)`.

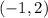Since
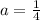`a=(1)/(4)` is positive

This means the vertex is the minimum point on the graph of the function.

The minimum y-value is 2.

The range is therefore
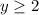`y\ge 2` or
`[2,+\infty)`

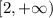
iii) To find the y-intercept, put
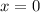`x=0` into the function.

`y=(1)/(4)|0+1|+2`

`y=(1)/(4)|1|+2`

`y=(1)/(4)+2`

`y=2.25`

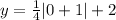
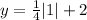
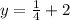
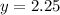
The y-intercept is (0,2.25) or
`b=2.25`

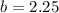
See attachment for graph.