Question

A spinner is divided into 4 sections. The spinner is spun 100 times. The probability distribution shows the results.

What is P(1≤x≤3) ?


Enter your answer, as a decimal.

Answer 1

P(1≤x≤3) defined the probability that the result is between 1 and 3, included. You can answer this question in two ways:

1. Sum the probabilities of good events:

From the graph, we have

`P(x=1) = 0.32,\quad P(x=2) = 0.24,\quad P(x=3) = 0.28`

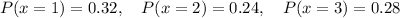
So,

`P(1\leq x \leq 3) = 0.32+0.24+0.28 = 0.84`

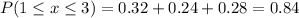
2. Use complementary probabilities

Asking that the result is 1, 2 or 3 is the same as asking that the result is not 4. The probability that the result is 4 is 0.16, so the probability that the result is not 4 will be

`P(x\\eq 4) = 1-P(x=4) = 1-0.16=0.84`

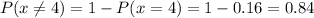
The result is obviously the same.