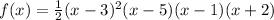Question

Find an equation for the polynomial P(x)

P
(
x
)
with y−
y
−
intercept at (0,45)
(
0
,
45
)
and roots: 3 (of multiplicity 2), 5, 1,-2

Answer 1

`f(x) = (1)/(2)(x -3)^2(x-5)(x-1)(x+2)`

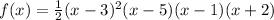
Explanation:

The equation of a polynomial has the factored form as:

`f(x) = a(x - r_1)(x-r_2)(x-r_3).....`

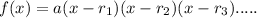
Since the roots here are 3, 5, 1, and -2, you take the opposite sign and place it in the equation. Where multiplicity is used this is the exponent of the factor.

`f(x) = a(x -3)^2(x-5)(x-1)(x+2)`

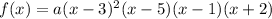
To find a, plug in the point (0,45) and solve for a.

`a(0 -3)^2(0-5)(0-1)(0+2) = 45\\a*9*-5*-1*2 = 45\\90a = 45\\a = 1/2`

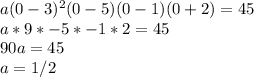
So the final equation is
`f(x) = (1)/(2)(x -3)^2(x-5)(x-1)(x+2)`