2 Answers

Otrejni · Answer 1 · 2020-07-06T02:51:24+0000

For this case, we have to factor the following expression:

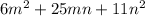
6m ^ 2 + 25mn + 11n ^ 2

The term that is in the middle must be rewritten as a sum of two terms whose product is:

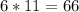
6 * 11 = 66

and whose sum is 25.

Those numbers are 22 and 3.

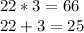
$22 * 3 = 66\\22 + 3 = 25$

Rewriting the term of the medium we have:

6m ^ 2 + 3mn + 22mn + 11n ^ 2

We factor the maximum common denominator of each group:

3m (2m + n) + 11n (2m + n)

We factor the polynomial by factoring the maximum common denominator,
(2m + n) :

(2m + n) (3m + 11n)

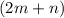Answer:

Please log in or register to add a comment.