Integration Formula:
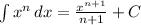
Integrate each term:
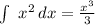
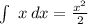
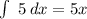
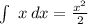
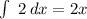
Altogether this becomes:
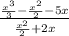
Your limits are 1 and 2. Substitute both numbers into the equation and minus them from each other.
x = 2:
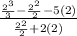
-
x = 1:
/(3) - (1)/(2)-5 )/( (1)/(2)+2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/v3908zyjv18binvula75gwciwnpigkmx06.png) [/tex]
[/tex]
x = 2:
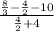
-
x = 1:
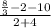
=
-1.212317928
Now convert all the answers to integers and see which one matches -1.212317928:
Because it's a negative number, we know it can only be A or B.
(A) = -1.212317928
(B) = -1.19047619
The answer is A:
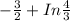
(A) - 3/2 = ln 4/3