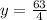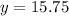Answer:
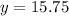
Explanation:
If y varies is jointly with
 and inversely as
and inversely as
![\sqrt[3]{z}](https://img.qammunity.org/2020/formulas/mathematics/high-school/uk4iv2byxrnoyhi1ojzn5qpm9jvboq57d6.png) , then you can write the following expression, where k is the constant of proportionality:
, then you can write the following expression, where k is the constant of proportionality:
![y=k*\frac{x^(2)}{\sqrt[3]{z}}](https://img.qammunity.org/2020/formulas/mathematics/high-school/5d9lbmqoifg5j9k3sjbdze4g1vyzdubuow.png)
If y=84, x=6 and z=27, you can find the constant of proportionality:
![k=y\frac{\sqrt[3]{z}}{x^(2)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/7701k5xsfpv2h93z6ndpj4sc5rwx98qi34.png)
![k=84\frac{\sqrt[3]{27}}{6^(2)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/2kr92ftwwcb9ve5tncxx4a4frjrhz614vy.png)
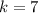
Then, when x=3 and z=64 y is:
![y=7(\frac{3^(2)}{\sqrt[3]{64}})](https://img.qammunity.org/2020/formulas/mathematics/high-school/5wi0l6ut6qt9cd394uughm69z9aoird8ji.png)