Answer:
Triangles OPQ and NPR are similar by AA Similarity Postulate
Explanation:
we know that
In this problem
NR is parallel to OQ
therefore
Triangles OPQ and NPR are similar by AA Similarity Postulate (the three internal angles are congruent)
because
<RNP=<QOP -----> by corresponding angles
<NRP=<OQP ----> by corresponding angles
<NPR=<OPQ
Remember that
If two triangle are similar, then the ratio of its corresponding sides is equal
Verify
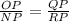
substitute the values
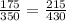
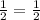 -----> is true
-----> is true
therefore
The triangles OPQ and NPR are similar