Answer:
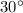
Explanation:
We are asked to find the measure of each exterior angle of a regular dodecagon.
We know that a regular dodecagon is a 12 sided regular polygon with each side equal.
We know that measure of each angle of n-sided regular polygon can be found using formula:
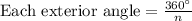
Upon substituting
 in above formula, we will get:
in above formula, we will get:
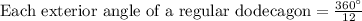

Therefore, the measure of each exterior angle of a regular dodecagon is 30 degrees.