Answer:
There are
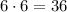 different ways to choose 4 screws such that 2 have a Phillips head and 2 have a slotted head.
different ways to choose 4 screws such that 2 have a Phillips head and 2 have a slotted head.
Explanation:
If 4 screws must be chosen so that 2 have a Phillips head and 2 have a slotted head, then you have to choose 2 screws with a Phillips head from 4 screws with a Phillips head and 2 screws with a slotted head from 4 screws with a slotted head.
You can choose 2 screws with a Phillips head from 4 screws with a Phillips head in
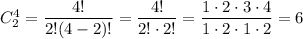
different ways.
You can choose 2 screws with a slotted head from 4 screws with a slotted head in
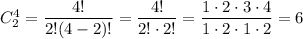
different ways.
In total there are
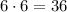 different ways to choose 4 screws such that 2 have a Phillips head and 2 have a slotted head.
different ways to choose 4 screws such that 2 have a Phillips head and 2 have a slotted head.