Question

the gravitational force between two objects is 45000 N. what will be the gravitational force between the two objects if the distance between the objects is reduced by one half​

Answer 1

If the distance is reduced by 1/2 and the masses don't change, then the force will increase by (2²) to 180,000 N .

Answer 2

The gravitational force between the two objects if the distance between the objects is reduced by one half​ is 180000 N.

Step-by-step explanation:

Given that,

Gravitational force = 45000 N

We need to calculate the gravitational force between the two objects

If the distance between the objects is reduced by one half​

We know that,

The gravitational force is equal to the product of the masses of the both objects divided by the square of the distance between the objects.

In form of formula

`F=(Mm)/(r^2)`

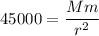`45000=(Mm)/(r^2)`.....(I)

If the distance between the objects is reduced by one half​

Then, the gravitational force will be

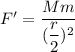`F'=(Mm)/(((r)/(2))^2)`....(II)

From equation (I) and (II)

`(45000)/(F')=((Mm)/(r^2))/((Mm)/(((r)/(2))^2))`

`(45000)/(F')=(1)/(4)`

`F=180000\ N`

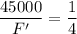
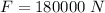
Hence, The gravitational force between the two objects if the distance between the objects is reduced by one half​ is 180000 N.