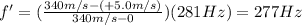Question

Part A cyclist is traveling at a constant velocity of 5.00m/s. The cyclist approaches a stationary musician playing a note frequency 281Hz. The air is still and the speed of sound is 340m/s. What is the frequency of the note that the cyclist hears?

A. 290Hz
B. 283Hz
C. 277Hz
D. 285Hz
Part B. A cyclist is traveling at a constant velocity of 5.00m/s. The cyclist approaches a stationary musician playing a note frequency 281Hz. The air is still and the speed of sound is 340m/s. What is the frequency of the note that cyclist hears after he passes the musician?
A. 270Hz
B. 277Hz
C. 274Hz
D. 284Hz

Answer 1

A) D. 285Hz

We can solve the problem by using the Doppler effect formula:

`f'=((v-v_o)/(v-v_s))f`

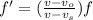
where

f' is the apparent frequency

v = 340 m/s is the velocity of the sound wave

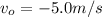`v_o = -5.0 m/s` is the velocity of the observer (the cyclist, in this case), which is negative because the cyclist is moving towards the sound source

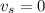`v_s = 0` is the velocity of the sound source (zero, in this case, since the musician is stationary)

f = 281 Hz is the original frequency

Substituting into the equation, we find:

`f'=((340 m/s-(-5.0 m/s))/(340 m/s-0))(281 Hz)=285 Hz`

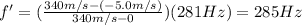
B) B. 277 Hz

Similarly, we can solve the problem by using the Doppler effect formula:

`f'=((v-v_o)/(v-v_s))f`

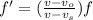
where

f' is the apparent frequency

v = 340 m/s is the velocity of the sound wave

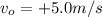`v_o = +5.0 m/s` is the velocity of the observer (the cyclist, in this case), which is now positive because the cyclist is moving away from the sound source

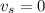`v_s = 0` is the velocity of the sound source (zero, in this case, since the musician is stationary)

f = 281 Hz is the original frequency

Substituting into the equation, we find:

`f'=((340 m/s-(+5.0 m/s))/(340 m/s-0))(281 Hz)=277 Hz`