Question

GEOMETRY HELP!

1. What is the length of BC?

2. What is the length of SU? Round rob the nearest tenth.

3. In the figure, All measurements are in inches. All angles are right angles. What is the length, in inches, of segment AC?

4. What is the measure of AB? What is the length of AD?

5. Kayla wants to find the width, AB, of a river. She walks along the edge of the river 100 ft and marks point C. Then she walks 22 ft further and marks point D. She turns 90 degrees and walks until her location and point A and point C are collinear. She marks point E at this location, as shown.

What is the width of the river? Round to the nearest foot.

Answer 1

1. Length of BC = 35

2. SU = 3.5

3. AC = 50 inches

4.

Part 1: AB = 10 cm

Part 2: AD = 2 cm

5. Width of River AB = 145.45 ft

Explanation:

1.

The length of BC is (x+4)+(2x+1) = 3x+5

Now, if we figure out x, we can plug that in and find length of BC.

Using similarity with the two triangles shown, we can set-up the ratio as:

`(8)/(12)=(x+4)/(2x+1)`

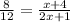
Now, cross multiplying and solving for x:

`(8)/(12)=(x+4)/(2x+1)\\8(2x+1)=12(x+4)\\16x+8=12x+48\\4x=40\\x=(40)/(4)=10`

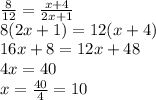
Now plugging in x=10 into 3x+5, we have 3(10)+5 = 35

Length of BC = 35

2.

Using pythagorean theorem in triangle PQT, we can solve for QT.

`(√(2))^2+(√(2))^2=QT^2\\2+2=QT^2\\4=QT^2\\QT=√(4)=2`

QT = RS = 2

Now using pythagorean theorem on Triangle RSU, we can solve for SU. So:

`RS^2+SU^2=RU^2\\2^2+SU^2=4^2\\SU^2=4^2-2^2\\SU^2=12\\SU=√(12)=3.5`

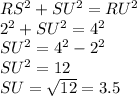
SU = 3.5

3.

If we draw a straight line as Segment AC, we have a right triangle with both legs measuring 30 and 40 inches, respectively. AC is the hypotenuse. Using pythagorean theorem, we can find out AC:

`AB^2+BC^2=AC^2\\30^2+40^2=AC^2\\2500=AC^2\\AC=√(2500)=50`

Thus AC = 50 inches

4.

AB:

We can set-up a similarity ratio to solve for AB. We can write:

`(12)/(20)=(6)/(AB)`

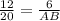
Now, cross multiplying, we can solve for AB:

`(12)/(20)=(6)/(AB)\\12AB=6*20\\12AB=120\\AB=(120)/(12)=10`

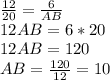
Thus, AB = 10 cm

AD:

We know, AB = BF + FD + DA

We also know, FD = 6, AB = 10 and BF & DA are same. So we can write DA in place of BF and solve. Thus:

`AB = BF + FD + DA\\10=AD+6+AD\\10-6=2AD\\4=2AD\\AD=2`

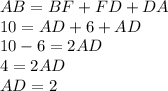
Thus, AD = 2 cm

5.

A single piece of information is missing from this problem. They have given DE = 32 ft.

Now, we see that triangle EDC is similar to triangle ABC, so their corresponding sides are proportional. Thus we can set-up a ratio as:

`(DC)/(BC)=(DE)/(BA)`

Now we can put the information we know and solve for AB, the width of the river.

`(DC)/(BC)=(DE)/(BA)\\(22)/(100)=(32)/(AB)\\22AB=32*100\\22AB=3200\\AB=(3200)/(22)=145.45`

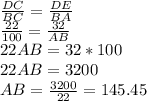
Width of River AB = 145.45 ft