Question

The equation for line passing through (6, 3) and (4, 1) could be written in slope-intercept form as 

Answer 1

`\boxed {\boxed {\sf E. \ y=x-3}}`

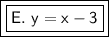
Explanation:

To find the equation of the line, we must first find the slope, then use the point-slope formula.

1. Find the Slope

The slope formula is the change in y over the change in x, or:

`m=(y_2-y_1)/(x_2-x_1)`

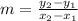
Where (x₁, y₁) and (x₂, y₂) are the points the line passes through.

The points given in the problem are (6,3) and (4,1). Therefore:

`x_1=6 \\y_1=3 \\x_2=4 \\y_2=1`

Substitute the values into the formula.

`m=(1-3)/(4-6)`

Solve the numerator.

• 1-3= -2

`m=(-2)/(4-6)`

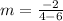
Solve the denominator.

• 4-6=-2

`m=(-2)/(-2)`

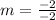
Divide.

`m=1`

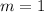
2. Find the Equation of the Line

We have the slope and a point, so we can use the point-slope formula.

`y-y_1=m(x-x_1)`

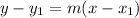
We know the slope is 1 and we can pick either point to use for (x₁, y₁). Let's use (4,1).

`y-1=1(x-4)`

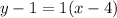
Distribute the 1.

`y-1=(1*x)+(1*-4)\\y-1=x-4`

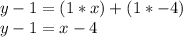
We want to find the equation in y=mx+b, so we must isolate the variable on one side of the equation.

1 is being subtracted from y and the inverse of subtraction is addition. Add 1 to both sides of the equation.

`y-1+1=x-4+1\\y=x-4+1\\y=x-3`

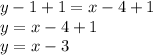
In slope-intercept form, the equation of the line is y=x-3