Question

a ball is thrown straight up into the air with a speed of 13 m/s. if the ball has a mass of 0.25 kg, how high does the ball go? acceleration due to gravity is g=9.8m/s^2

Answer 1

Hello!

The answer is: 8.62m

Why?

There are involved two types of mechanical energy: kinetic energy and potential energy, in two different moments.

First moment:

Before the ball is thrown, where the potential energy is 0.

Second moment:

After the ball is thrown, at its maximum height, the Kinetic Energy turns to 0 (since at maximum height,the speed is equal to 0) and the PE turns to its max value.

Therefore,

`E=PE+KE`

Where:

`PE=m.g.h`

`KE=(1*m*v^(2))/(2)`

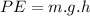
E is the total energy

PE is the potential energy

KE is the kinetic energy

m is the mass of the object

g is the gravitational acceleration

h is the reached height of the object

v is the velocity of the object

Since the total energy is always constant, according to the Law of Conservation of Energy, we can write the following equation:

`KE_(1)+PE_(1)=KE_(2)+PE_(2)`

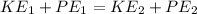
Remember, at the first moment the PE is equal to 0 since there is not height, and at the second moment, the KE is equal to 0 since the velocity at maximum height is 0.

`(1*m*v^(2))/(2)+m.g.(0)=(1*m*0^(2))/(2)+m.g.h\\(1*m*v_(1) ^(2))/(2)=m*g*h_(2)`

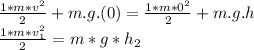
So,

`h_(2)=(1*m*v_(1) ^(2))/(2*m*g)\\h_(2)=(1*v_(1) ^(2))/(2g)=(((13m)/(s))^(2) )/(2*(9.8m)/(s^(2)))\\h_(2)=8.62m}`

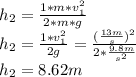
Hence,

The height at the second moment (maximum height) is 8.62m

Have a nice day!