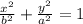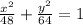QUESTION 1
The given ellipse has equation:
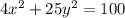
Divide through by 100 to get;
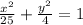
The ellipse has it major axis on the x-axis.

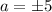
The vertices is
(-5,0) and (5,0).
Also
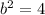
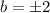
The co-vertices are,
(0,-2), (0,2).
We use
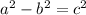



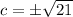
The foci:
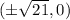
We plot all these points and graph our ellipse.
See attachment
QUESTION 2.
If the ellipse has a vertex at
(0,-8) and a focus at (0,4) then
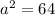
and
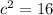
we can use
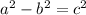
to determine the value if b.

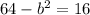
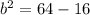

The equation of the ellipse is