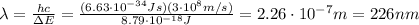(a) 159 nm
First of all, let's calculate the energy difference between the level E1 and E4:
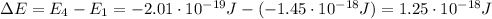
Now we know that this energy difference is related to the wavelength of the absorbed photon by
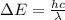
where
 is the Planck constant
is the Planck constant
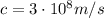 is the speed of light
is the speed of light
 is the wavelength of the photon
is the wavelength of the photon
Solving for
 , we find
, we find
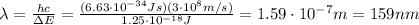
b) 293 nm
As done in part a), let's calculate the energy difference between the level E2 and E3:
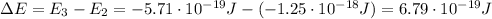
this energy difference is related to the wavelength of the absorbed photon by
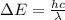
Solving for
 again, we find
again, we find
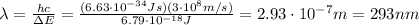
c) 226 nm
As done in part a) and b), let's calculate the energy difference between the level E1 and E3:
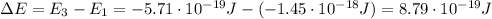
this energy difference is related to the wavelength of the emitted photon by
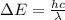
Solving for
 again, we find
again, we find