1. Start the search among 2-digit numbers. A dropdown number (DDN) with 2 digits is a number
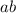 such that
such that
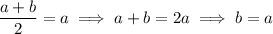
or
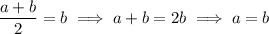
but both of these solutions violate the requirement that the digits are distinct, so there are no 2-digit DDNs.
A 3-digit DDN
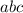 is such that
is such that
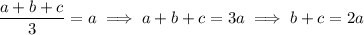
or
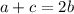 if the average is
if the average is
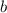 , or
, or
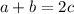 if the average is
if the average is
 . The smallest possible value for
. The smallest possible value for
 is 1 since we require 3 digits. Then
is 1 since we require 3 digits. Then
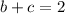 , and we can pick
, and we can pick
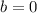 and
and
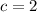 to get the smallest DDN, 102.
to get the smallest DDN, 102.
2. In a 4-digit DDN
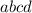 , we have
, we have
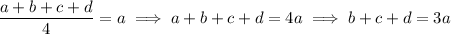
or
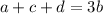 or
or
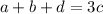 or
or
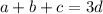 .
.
We're free to fix
 and
and
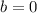 to try to get the smallest DDN. This leaves us with
to try to get the smallest DDN. This leaves us with
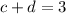 or
or
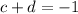 or
or
 or
or
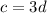 .
.
The first two cases are impossible - the only choices for
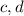 such that
such that
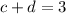 are 1 and 2, and the sum of two positive integers must be positive. The smallest possible value of
are 1 and 2, and the sum of two positive integers must be positive. The smallest possible value of
 is 2; this leaves us with
is 2; this leaves us with
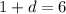 or
or
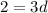 , but the latter case is impossible because 3 does not divide 2. So
, but the latter case is impossible because 3 does not divide 2. So
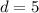 , and the smallest 4-digit DDN is 1025.
, and the smallest 4-digit DDN is 1025.
To find the largest DDN, start with the largest possible values for
 and
and
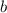 . Let
. Let
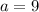 and
and
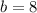 . Then
. Then
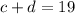 or
or
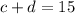 or
or
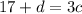 or
or
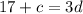 . At most, we can have
. At most, we can have
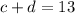 with 7 and 6, so the first two cases are impossible. If we maximize
with 7 and 6, so the first two cases are impossible. If we maximize
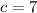 , then either
, then either
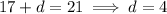 or
or
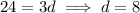 (which we don't want). So the largest 3-digit DDN is 9874.
(which we don't want). So the largest 3-digit DDN is 9874.
3. I don't have an analytical solution to this, but using brute force (program) the total count is 112.
4. It is possible; consider 1249 and 1250, with digital averages
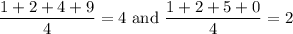
which happens to be the smallest pair. (Also found with brute force.)