Question

HELP. How long is the minor axis for the ellipse shown below?

Answer 1

Given:

The equation of ellipse is

`((x+4)^2)/(25)+((y-1)^2)/(16)=1`

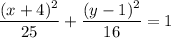
To find:

The length of the minor axis.

Solution:

The standard form of an ellipse is

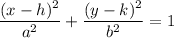`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1` ...(i)

where, (h,k) is center, if a>b, then 2a is length of major axis and 2b is length of minor axis.

We have,

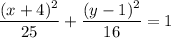`((x+4)^2)/(25)+((y-1)^2)/(16)=1` ...(ii)

On comparing (i) and (ii), we get

`b^2=16`

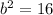
Taking square root on both sides.

`b=\pm 4`

Consider only positive value of b because length cannot be negative.

`b=4`

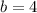
Now,

Length of minor axis =
`2b`

=
`2(4)`

=
`8`

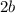
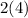
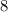
So, the length of minor axis is 8 units.

Therefore, the correct option is B.