Question

For the function f(x) = -2(x + 3)^2 - 1, identify the vertex, domain, and range.​

Answer 1

vertex (-3 , - 1)

domain : all real number

range: y <= -1

Explanation:

y = a(x-h)^2 + k where vertex (h, k)

In this case

f(x) = -2(x + 3)^2 - 1 , h = - 3 and k = -1

So vertex (-3 , - 1)

Since a = - 2<0, the function is downward and has maximum = -1

So Domain : all real number and range: y <= -1

Answer 2

Vertex (-3,-1)

Domain :set of real numbers

Range:=(
`-\infty,-1]`

Explanation:

We are given that a function

`f(x)=-2(x+3)^2-1`

We have to find the vertex , domain and range of given function.

We know that equation of parabola whose vertex at (h,k) is given by

`y=a(x-h)^2+k`

Compare with the given equation then we get

Vertex=(-3,-1)

`y=-2(x+3)^2-1`

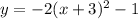
Substitute x=-3 then we get

y=-1

Domain:all real numbers because given function is defined for all real numbers.

Range=(-infinity, -1]

Therefore, domain of f(x)=R

Range=(-
`\infty, -1]`