The fulcrum should be placed 0.44 from the 12 N weight or 0.56 m from the 8 N weight.
Step-by-step explanation:
Given:
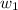 = 8 N
= 8 N
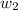 = 10 N
= 10 N
Since the meter stick has a length of 1 m, and
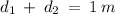
Let
 = x
= x
Let
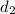 = 1 - x
= 1 - x
Question:
Where should the fulcrum be placed to have the meterstick balanced?
Equation:
For the system to be balanced, the product of the weight and distance of the objects on opposite sides should be equal. This is is shown by the equation:
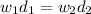
where: w - weight
d - distance from the fulcrum
Solution:
Substituting the value of
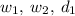 and
and
 in the formula,
in the formula,
(8 N)(x) = (10 N)(1 m - x)
x(8 N) = (10 N)m - x(10 N)
x(8 N) + x(10 N) = (10 N) m
x(18 N) = 10 N
x =
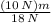
x = 0.56
Solve for

 = x
= x
 = 0.56 m
= 0.56 m
Solve for
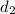
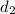 = 1 m - x
= 1 m - x
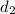 = 1 m - 0.56 m
= 1 m - 0.56 m
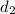 = 0.44 m
= 0.44 m
Final Answer:
The fulcrum should be placed 0.44 from the 12 N weight or 0.56 m from the 8 N weight.