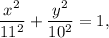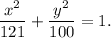Answer:
1.
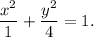
2.
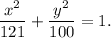
Explanation:
The equation of the ellipse is
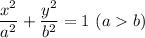
or
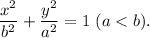
1. If the vertex of the ellipse is at point (0,2), then b=2.
If the co-vertex of the elllipse is at point (-1,0), then a=1.
The equation of the ellipse is

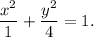
This ellipse has foci on y-axis.
2. If the vertex of the ellipse is at point (-11,0), then a=11.
If the co-vertex of the elllipse is at point (0,10), then b=10.
The equation of the ellipse is