Part 1 :
P = $200
r = 3.5% or 0.035
t = 3
n = 4
Compound interest formula =
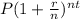
=
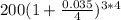
=
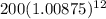
=
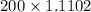
= 222.04
So, money in the bank will be = 200+222.04 = $422.04
Part 2 :
P = $200
r = 3.5% or 0.035
t = 3
Continuous compound interest formula is =
A =
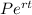
Putting e = 2.71828 we get.
A =
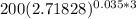
=
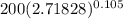
= 200*1.11071 = 222.14
Hence, amount in account after 3 years will be= 200+222.14 = $422.14