Question

Find the angle between the vectors.
U=< -4,-3>
V = < -1,5>

Answer 1

Explanation:

The formula for the angle between vectors

`\alpha = \cos {}^( - 1) ( (uv)/( |u| |v| ) )`

To multiply vectors, multiply the first component and multiply the second component and add them.

(-4*-1) + (-3*5)= 4-15=-11.

To find magnitude of vectors, use the Pythagorean theorem

`u = \sqrt{ { - 4}^(2) + { - 3}^(2) } = 5`

`v = \sqrt{ - 1 {}^(2) + 5 {}^(2) } = √(26)`

so

`|u| |v| = 5 √(26)`

Know we have,

`\alpha = \cos {}^( - 1) ( (7)/(5 √(26) ) )`

`\alpha = 105.94`

in degrees,

`\alpha = 1.849`

in radians

Answer 2

115.6° (1 d.p.)

Explanation:

To find the angle between two vectors:

• Create a triangle with the vectors as two sides and the included angle θ between them.
• Find the magnitude of each vector (the length of each side of the triangle).
• Use the cosine rule to find the angle θ.

**Please see attached for the triangle diagram**

Given vectors:

`\textbf{u}=-4\textbf{i}-3\textbf{j}`

`\textbf{v}=-\textbf{i}+5\textbf{j}`

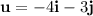
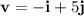
Use Pythagoras Theorem to find the magnitude of each vector:

`\implies |\textbf{u}|=√((-4)^2+(-3)^2)=5`

`\implies |\textbf{v}|=√((-1)^2+5^2)=√(26)`

`\overrightarrow{\text{UV}}=\textbf{v}-\textbf{u}=(-\textbf{i}+5\textbf{j})-(-4\textbf{i}-3\textbf{j})=3\textbf{i}+8\textbf{j}`

`|\overrightarrow{\text{UV}}|=√(3^2+8^2)=√(73)`

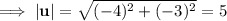
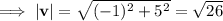
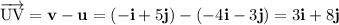
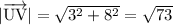
Cosine Rule (for finding angles)

`\sf \cos(C)=(a^2+b^2-c^2)/(2ab)`

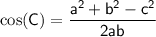
where:

• C = angle
• a and b = sides adjacent the angle
• c = side opposite the angle

Find angle θ using the cosine rule:

`\implies \cos(\theta)=\frac{|\textbf{u}|^2+|\textbf{v}|^2-|\overrightarrow{\text{UV}}|^2}{2|\textbf{u}||\textbf{v}|}`

`\implies \cos(\theta)=(5^2+\left(√(26)\right)^2-\left(√(73)\right)^2)/(2(5)\left(√(26)\right))`

`\implies \cos(\theta)=(-22)/(10√(26))`

`\implies \theta=\cos^(-1)\left((-22)/(10√(26))\right)`

`\implies \theta=115.5599652...^(\circ)`

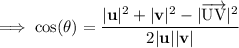
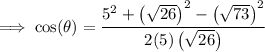
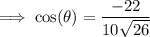
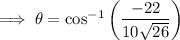
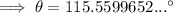
Therefore, the angle between the vectors is 115.6° (1 d.p.).