Answer:
See explanantion
Explanation:
Consider the equation
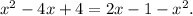 This equation consists of two parts:
This equation consists of two parts:
- left part is defined by the function
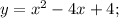
- right part is defined by the function
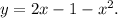
Both these functions are quadratic and determine parabolas. The graph of the function
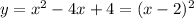
is parabola tangent to x-axis at point (2,0) with branches going up. The graph of the function
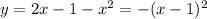
is parabola tangent to x-axis at point (1,0) with branches going down (see diagram). As you can see from the diagram these two parabolas do not intersect, then there are no solutions.