Final Answer:
1. The value of r is 15.
2. The sine of the angle is 0.8.
3. The cosine of the angle is 0.6.
4. The tangent of the angle is
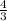 or approximately 1.33.
or approximately 1.33.
5. The angle is 36.87°.
Step-by-step explanation:
To determine r in the Cartesian coordinate system, we use the Pythagorean theorem,
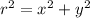 . Given the point (9, 12),
. Given the point (9, 12),
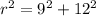 . Calculating this,
. Calculating this,
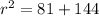 , and
, and
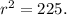 Taking the square root of both sides,
Taking the square root of both sides,
 Therefore, the value of r is 15.
Therefore, the value of r is 15.
The sine of an angle in standard position is defined as
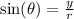 . In this case,
. In this case,

The cosine of an angle is defined as
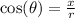 . In this instance,
. In this instance,

The tangent of an angle is given by
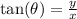 . For this point,
. For this point,
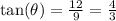 , which is approximately 1.33.
, which is approximately 1.33.
Finally, to find the angle
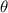 , we use the arctangent function:
, we use the arctangent function:
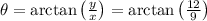 . Calculating this, we find
. Calculating this, we find
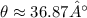 . Therefore, the angle is approximately 36.87°.
. Therefore, the angle is approximately 36.87°.