Answer: Yes, radicals can be rationals.
Explanation:
Yes, a radical can be rational.
If a square root is a perfect square, you will obtain an integer, and by definition, the integer are rationals (they can be written as simple fractions).
Example:
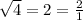
If the radical has a root n and number inside of the root can be written as a power with exponent
 , then you will obtain a radical.
, then you will obtain a radical.
Example:
![\sqrt[3]{64}=\sqrt[3]{4^(3)}=4=(4)/(1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/40wkr320dcmj87yx73wglwxwvpjlotmlad.png)