Question

Which is the graph of linear inequality 6x + 2y > –10?..​

Answer 1

weres the graphs

Explanation:

Answer 2

Explanation:

`6x+2y>-10\qquad\text{subtract 6x from both sides}\\\\2y>-6x-10\qquad\text{divide both sides by 2}\\\\y>-3x-5`

Change the inequality symbol to the symbol of equation.

`y=-3x-5`

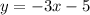
Choice any two values of x and calculate the values of y:

for x = 0

`y=-3(0)-5=0-5=-5\to(0,\ -5)`

for x = -2

`y=-3(-2)-5=6-5=1\to(-2,\ 1)`

Draw the line passing through the given points.

If is < or >, then plot the dot line.

If is ≤ or ≥, then plot the solid line.

We have the sign of an inequality ">". Therefore plot a dot line.

Now shading.

If is < or ≤, then shading to the left.

If is > or ≥, then shading to the right.

We have the sign of an inequality ">'. Therefore shading to the right.