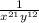Answer:
B)
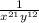
Explanation:
The given expression is
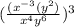
Now we can bring the power 3 inside the bracket using the rule
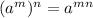
=
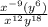
Now we have to use the quotient rule and simplify it.
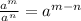
Using the above rule, we get
=
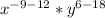
=

Since we have a negative exponent. We can rewrite using the rule a^-m = 1/a^m
=
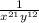
Therefore the answer is B)