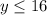Question

The function f(x)=-x^2-2x+15 is shown on the graph. What are the domain and range of the function?

Answer 1

domain is set of all real numbers

Range is
`y\leq 16`

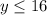
Explanation:

`f(x)=-x^2-2x+15`

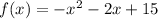
Domain is the set of x values for which the function is defined

In f(x), we have y values for all x values, So there is no restriction for x

Hence domain is set of all real numbers

Range is the set of all y values for which the function is defined

From the graph of the given function f(x), the maximum point that is vertex at (-1,16)

The range of the function is y<=16

Range is
`y\leq 16`

Answer 2

Domain is all real numbers

y ≤ 16

Explanation:

The domain is the set of x values that the graph covers. There is no restriction on the x values. The domain is all real numbers.

The range is the set of y values that the graph covers. The highest the y values go is 16 at the top of the parabola. So the range is y ≤ 16.