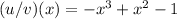Question

If u(x)=x^5-x^4+x^2 and v(x)=-x^2, which expression is equivalent to (u/v)(x)?

Answer 1

x^3-x^2+1

Explanation:

u(x)=x^5-x^4+x^2

v(x)=-x^2

(u/v)(x) = (x^5-x^4+x^2) /x^2

= (x^5/x^2) - (x^4 /x^2) +(x^2/x^2)

= x^(5-2) - x ^(4-2)+ x ^(2-2)

=x^3-x^2+1

Answer 2

`(u/v)(x)=-x^(3)+x^(2)-1`

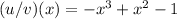
Explanation:

The arithmetic operation of the two equations presented in this case can be solved as a division of polynomials.

We can write the problem as:

`(u/v)(x)=(u(x))/(v(x)) \\\\(u/v)(x)=(x^5-x^4+x^2)/(-x^2)`

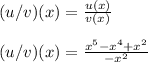
We need not to forget the negative in the denominator. Then we can factor the numerator as follows:

`(u/v)(x)=((-x^2)(-x^3+x^2-1))/((-x^2))`

Now we can easily spot the solution, and get there with the following steps:

`(u/v)(x)=((-x^2)/(-x^2)) (-x^3+x^2-1)\\\\(u/v)(x)=(1)(-x^3+x^2-1)`

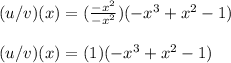
As I said earlier we need to remember that the negative will change the symbols in the equation once we factor the polynomial.

And like that we get to the answer:

`(u/v)(x)=-x^(3)+x^(2)-1`